If you missed the first part of this story, click here and then come back!
So now that we know that there is a significant problem with how our students view the equals sign, how do we implement the suggestions put forth in Part 1 of this blog? How do we get students to understand that the equals sign means a relation between values on either side of the equals sign? I think following the sequence detailed below is a better approach to instruction than what is currently being followed in elementary curriculum.
If we could determine how operational and relational symbols are introduced to our students, I would teach a unit in the following sequence.
Step 1 – Develop Relational Vocabulary
Introduce the phrases “greater than” and “less than.” Have students make connections with scenarios in which we compare quantities and amounts without even introducing numbers or symbols. Introduce the words greater than and less than.
Introduce the word “equals.” Delay introducing the word “equals” until after students have a deeper understanding of the idea of greater than and less than. Allow students to grapple with how to describe the sameness between groups of objects. Then introduce the word equals.
Step 2 – Link Relational Vocabulary to Counting and Cardinality
Have students count two sets of objects within 10 and compare each set verbally by saying more, same, less, and then moving into the more formal words of greater than, less than, or equals to.

Step 3 – Link Relational Vocabulary with Relational Symbols
Introduce notation with the equals sign
Pose story problems in which there is an equal amount such as this one about James and Carla.
Have students discuss the comparison of the number of apples James and Carla each have. Then model for the student that since James and Carla both have an equal number of apples, we can write it as shown below.
7 = 7
This is an important opportunity for teachers to model that it is not always necessary to notate using operational symbols. This is important because we know that students view the = as though it is the enter button on the calculator (which implies a command to do something). When students view the = this way, they are adamant that 7 = 7 is not a true equation because there is not a plus or minus sign.
Pose story problems in which there is not an equal amount. An example is included in the pdf mentioned at the end of this blog.
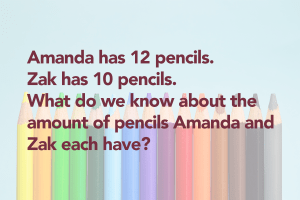
Introduce Greater Than and Less Than Symbols
Pose story problems such as this one about Amanda and Zak. In this problem students are comparing two numbers where one is greater than the other.
Some additional questions such as, “Does one person have a greater amount than the other? Who has less? Who has the greater amount?” can be asked to push students deeper into their understanding.
The teacher then introduces and models notating with the > symbol and writes the following inequality.
12 > 10
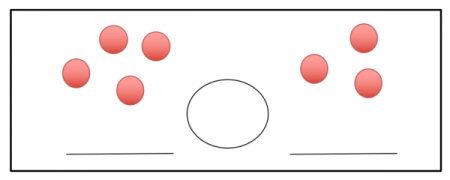
Show students sets of objects, like the diagram below. Students first write the quantity for each group of objects and then insert the symbol between each group of objects that makes each statement true.
Step 4 – Introduce Operational Symbols
Before showing students equations such as 3 + 5 = 8, first expose students to story problems that involve an action. As you present the problem, focus only on the action and operational symbol related to that action. Here, the question in the problem has intentionally been excluded from the problem.
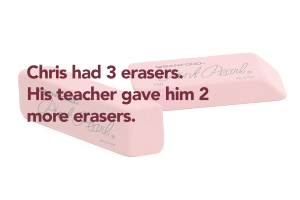
Read and discuss with students the story in the problem. Then model for students that we can write an expression such as 3 + 2 to show what is happening in the problem.
Step 5 – Introduce Students to Equations Involving Both Relational and Operational Symbols
Write equations to match story problems. Pose story problems that show one action as shown in the examples on the right. Have students write equations to match the story problem using a box or blank space for the unknown in the problem. In Chris’ problem, students may write 3 + 2 = ____.
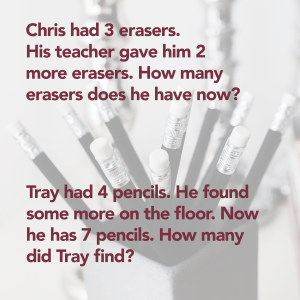
True and False Statements. Pose true and false statements seen to the right. Ask students to determine if each statement is true or false and to explain their reasoning. At a minimum, these statements should be shown to students as early as first grade.
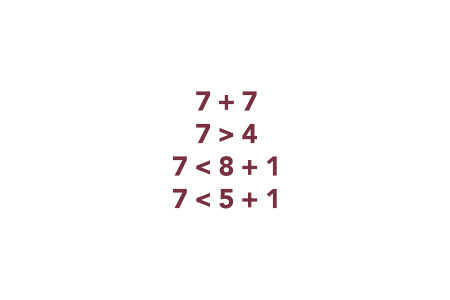
Relational statements with unknown numbers. Pose statements that include unknown numbers, like in the image shown below.
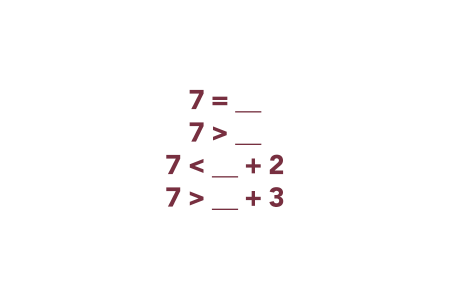

Write equations to match story problems with two actions. I recommend posing story problems containing two actions and a comparison, like you see on the right. Then, have students write equations to match the story problem.
Ask, “How could we represent the action in James’ problem? What about Carla’s problem?” Then, write the following on the board as shown.
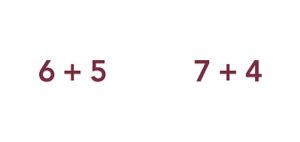
Ask, “After James and Carla both put more apples into their bags, who had more apples? How many apples did James have? How many apples did Carla have? How could we write the comparison of the number of apples each had? If they had the same amount, could we insert an equals sign between ‘6 + 5 and 7 + 4?’ ”
Discuss why it is okay for equations to have more than one plus sign.
True and false statements with at least four numbers. Pose True and false statements similar to what you see below. Ask students to determine if each statement is true or false and to explain their reasoning. Students should become comfortable with statements like these at first grade, if not sooner.
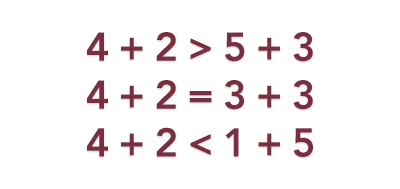
Relational statements with at least four numbers. Pose statements that include unknown numbers as seen below.
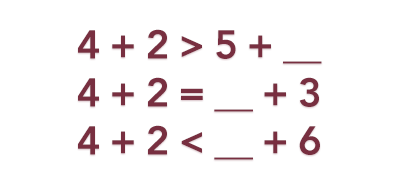

According to most state curriculum standards for mathematics, first graders are expected to be proficient at using these symbols. Knowing the names of the symbols is important, but it is also important for students to understand that the = symbol is similar to the < and > symbols because all three are relational symbols. It’s equally important for students to understand that in the equation 3 + 4 = 7, the addition symbol signifies an action, or an operation. However, the = sign is signifying a relation between the left and right sides of the equals sign. In other words, the = sign is not a command to perform the operation on its left-hand side.
For a more detailed list of ideas and additional examples in a printer friendly format, click here. As a note, I do recommend instructionally following the order listed in the pdf link.
