Have you ever noticed that the = button on a calculator means something different than how we use = on paper? Unfortunately, our elementary students tend to view the equals sign just as if they were pressing the enter button on a calculator. In other words, they have an operational view of the equals sign. Take for example the following equation.
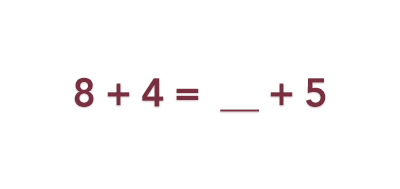
Students with an operational view of the equals sign often answer 12, because 8 + 4 equals 12. However, they are not understanding that if we answer with 12, then the full equation says that the sum of 12 + 5 is equal to the sum of 8 + 4. What we want our math students to understand is that the sum of the left side of the equation must be equal to the sum of the right side of the equation. In other words, the missing number is 7, because both sides would then be equal to 12.
But why do students get this partial understanding of the equals sign, and how do we fix this issue? With elementary mathematics standards specifically addressing the intended meaning of = in mathematics, why are so many students still struggling with the meaning of the equals sign? I think it is because we are not teaching students to view the equals sign as a relational symbol.
In this post, I will refer to the +, –, x, and ÷ symbols as operational symbols. I will refer to the <, >, and = symbols as relational symbols.
In my experiences both in teaching elementary students and working with teachers, I have seen students as early as kindergarten being shown the equals sign in equations such as 2 + 3 = 5 before they have a solid understanding of what mathematicians have decided the = means. Why do we jump so quickly into using mathematical symbols like the equals sign before students actually understand the meaning behind the symbol?
For the last six years, I have interacted with hundreds of students and dozens of teachers around the topic of the meaning of equals sign. We have posed numerous problems trying to study how students view the equals sign. A common theme is that despite students improving in their understanding of the equal sign, there are some pretty significant misconceptions still present.
I have come to think that we should slow down our introduction of these abstract symbols and instead go deeper into understanding the meanings of greater than, less than, equals, plus, and minus before exposing students to the operational and relational symbols.
If I could determine how operational and relational symbols are introduced to our students, I would suggest the following five steps.
- Step 1 – Develop Relational Vocabulary
- Step 2 – Link Relational Vocabulary to Counting and Cardinality
- Step 3 – Link Relational Vocabulary with Relational Symbols
- Step 4 – Introduce Operational Symbols (Only after students’ understanding of relational symbols is established)
- Step 5 – Introduce Students to Equations That are Comprised of Both Relational and Operational Symbols
To see an example for each category of development, as well as to see a more detailed explanation and list of ideas, check out part 2!
Join us in this discussion! What are you doing to help your students to develop a stronger understanding of the equals sign? Share your ideas in the comments, tweet at us at @teachingsolves and tag the #tips_blog hashtag!
