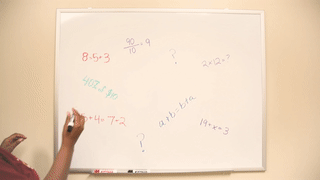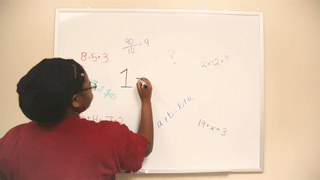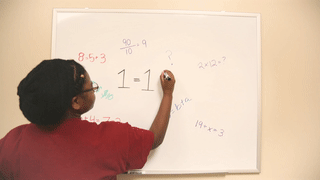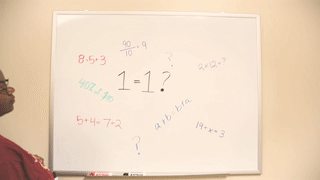
Pop quiz: True or false? 1=1. You’re probably thinking, “Of course it’s true! Obviously 1 equals 1!”
Is it really obvious, though? I’d like to think that this statement is true as well. I would also like to think that my 7-year-old self would have said the same thing. However, that may not be the case for little-me or other first-grade students.
Let’s try another one: Read this equation and decide whether it is true or false.
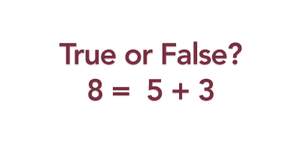
8 = 5 + 3. It’s a no-brainer, right? The quantity ‘8’ is equivalent to itself, which in this case looks like ‘5 + 3’, so this, again, is true. Now imagine you’re back in second grade. Your teacher is writing an equation on the board (or over-head projector, remember those?) like this one. Is the problem written as or?
There’s not much difference between the two equations, but most elementary students see equations like 5 + 3 = 8 much more often than ones like 8 = 5 + 3. If you saw the first orientation of that equation a lot in elementary school, raise your hand. Now that most of you are raising your hand, let’s take a moment to think. If this orientation was the only way you ever saw equations throughout elementary school, how would you react to the previous question?
What seems true to us now may not have seemed to be “true” when we were young. The rules didn’t change, our understanding of the rules did! That includes how we reason through math questions.
In 2014 and 2015, a team of researchers conducted more than 1,500 student interviews to see how students reason through math questions, including true/false questions like the ones above. I was one of the assistant researchers who coded videos of the student interviews to document how kids were thinking about the math problems. I later transcribed student responses to several true/false questions about equations. In this blog post, I’ll discuss three true/false questions in particular that I thought had intriguing answers; you may find the result and response to be surprising. I sure did!

A similar true/false question to 1=1 was asked in the interviews with first- and second- graders. Approximately 68% of the students from the transcribed interviews said the statement was “true”. There were variations in reasoning, but the most common response was that they are the same number, as in the quantity ‘1’ is equivalent to itself. Yay! This is good, two thumbs up!
But let’s not get ahead of ourselves yet – more than 30% of the students said the statement was false. Why? Because there was no ‘plus or minus’ sign. These students noted that the equation didn’t include an addition or subtraction sign, so there have been something wrong with the equation. Little-me (and maybe little-you!) would have probably noticed the same thing.
So how about the 8 = 5 + 3 problem? A similar true/false question was asked in the interviews and, once again, many of the students said “true,” but this time only 53% of them said it was true. The reasoning was that the quantity ‘8’ is equivalent to ‘5’ added to the quantity ‘3’ (or the reverse). Students would use their fingers or manipulatives to confirm this statement. Other students said it was true, but that the equation was “backwards” or “switched around” –interesting!
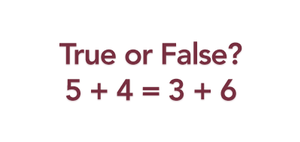
On the flip side for students who said it was false, their common reasoning was that ‘8’ does not equal ‘5’. Another explanation was that the equals sign and the addition sign were in the wrong place. Kind of similar to students who noticed that the equation was “backwards,” but these students said that it made the statement false.
Pop quiz again: does 5 + 4 = 3 + 6? I’ll admit; it’s a bit of a head-scratcher if you’re not paying attention, but the sum of ‘5 + 4’ is equivalent to the sum of ‘3 + 6’. So this statement is true.
You might have guessed by now: not many students (only 31%) got the question like this one correct. The students who said the statement was true mostly said that each side is ‘9’, so overall, the equation is true. However, a lot of students who stated it was false said that ‘5 + 4’ does not equal ‘3’. Oddly enough, even when they calculated both sides of the equation (with their fingers or blocks) to be ‘9’, many students stuck with their original answer.
Are you surprised by the results? I was and wasn’t at the same time. This study found that some elementary mathematics curricula do not expose students to “nonstandard equation types.” Exposure to these types of equations can make a difference in how students answer and reason these true/false questions.
Let me know what you think! Were you surprised with some of the ways students are explaining these true/false questions? If you can recall, how did you reason with these true/false questions? It’s okay if little-you would not have given the correct response. I know little-me wouldn’t have, and that’s okay!
Lastly, please use the comments section (or send us a tweet and tag #tips_blog) to share some teaching strategies that can help students think beyond these types of reasoning. Every little bit of effective advice can go a long way!
