What topic in elementary math is so important for later achievement and yet so little understood?
If you think the answer is “fractions,” you are not alone. Research suggests that building a solid foundation for fraction understanding is one of the strongest predictors of student achievement in mathematics in middle and high school (Siegler et al., 2012).
Unfortunately, students can appear to know a lot about fractions without really having a deep conceptual understanding of them. They may not understand fractions as numerical quantities or the relationship between numerator and denominator. Indeed, recognizing this relationship is key since it leads to an understanding of fraction as division and later of rational numbers and proportional thinking.
Instead, students are often taught “tricks” for performing operations on fractions. One common example of this kind of fraction instruction is when students are told, without further explanation, to solve 1/2 ÷ 1/3 using the phrase “keep, change, flip” (i.e., keep the first fraction, change the operation to multiplication, and flip the second fraction) so that
1/2 ÷ 1/3 becomes 1/2 x 3/1
This procedural knowledge only carries them so far as they move into higher-level math before they hit a wall and have to go back and fill gaps in fraction understanding. Over time, it is easy for students to forget a “trick” or to confuse mnemonic devices for operating on fractions, leaving them with no conceptual knowledge to use in finding a solution nor a way to know whether their calculations make sense. For instance, we have seen students try to solve 100x/(-2) by trying to apply the “keep, change, flip” rule by doing this:
100x (2)=200x
In this case, the student “kept” the first term and “changed” the operation to multiplication, but they did not understand the difference between “flipping” a fraction into its reciprocal and “flipping” the sign of a number—a common mistake (Cardone, 2015).
One way to create a strong foundation in fractions is to use equal-share problems. They are like a Swiss Army knife of math problems because they are versatile enough to assess understanding of fractions from as early as kindergarten and on through high school and beyond.
With strategic use of numbers, equal-share problems can be used as a tool to help a teacher assess student understanding of fractions and, in turn, to help students improve their understanding. For example, one could start with a basic “4 children share 10 brownies” problem to observe whether or not students recognize that a whole unit can be broken into smaller parts or that students can create and name fractional quantities. This problem can also assess the understanding of several unit-fraction ideas that are key to the development of operations with fractions.
Did you know?
Florida’s new B.E.S.T. math standards include the understanding of the unit fraction beginning in grade 3 (MA.3.FR.1), which supports the idea of building this concept as the cornerstone of understanding fractions. The unit fraction idea reappears in the B.E.S.T. in grade 5 and again in the notes for the high-school standards.
If we find that students are not able to demonstrate their understanding of these beginning concepts, then we can continue to use equal-share problems to help develop and/or strengthen these basic concepts. For instance, when solving the “4 children share 10 brownies” problem, perhaps one of the students answered “everyone gets ten one-fourths” and wrote:
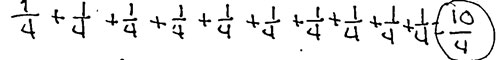
while another drew squares to represent the solution as:
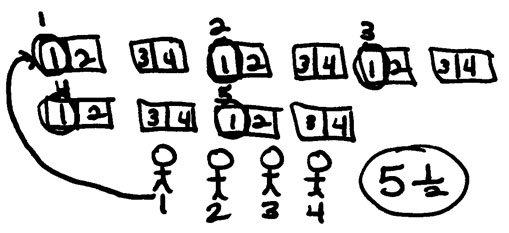
Notice that, in the second example, the student wrote "5 1/2" ” as the solution. At first glance, this may look incorrect; however, it is important to further examine the drawing and listen to the student’s explanation to assess if the answer is right or not. Perhaps the student, after prompted, would say “each child gets five one-half pieces” or “each child gets five halves.” Students’ use of fraction notation does not come naturally but develops gradually through pictures, words, and the learning of standard fraction terminology. In this case, the notation used in the second drawing presents an opportunity for the teacher to help students make a connection between "5 1/2" and ½+½+½+½+½= 5/2 and even to 5 x 1/2= 5/2.
The utility of the equal-share problems becomes evident when we see that this same problem, “4 children sharing 10 brownies,” can also be used to highlight fraction equivalency. Using these same answers, we can ask students if the two solutions above are the same and to explain their reasoning. In this manner, we build on their own knowledge and guide students through fraction equivalence to an understanding of fraction as division and later of rational numbers as fractions of the form a/b when b≠0
The discussion also provides us, as their teacher, even more information about their understanding of related ideas.
No teacher should leave home without this Swiss Army knife!
Reference
Cardone, T. (2015, March 2). Reason why when you invert and multiply. https://www.nctm.org/Publications/Mathematics-Teaching-in-Middle-School/Blog/Reason-Why-When-You-Invert-and-Multiply
Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., Susperreguy, M. I., & Chen, M. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23, 691–697. https://doi.org/10.1177%2F0956797612440101
